Trable s koláči
Intuitivně každý chápe, že jeden celý koláč je jeden celek. Že představuje 100 % a lze ho rozdělit na různě velké dílky, z nichž lze sestavit zase jen jeden koláč (pokud někdo kousek nesní). A přesto se občas stává, navzdory neúprosné logice, že autorům vznikne (zcela nesmyslně) více než jeden koláč. A existují i další případy, kdy jsou koláčové grafy použity nevhodně, nebo dokonce nesprávně. Uveďme tři příklady.
Každý koláč „chutná“ jinak!
Začněme tím nejjednodušším, spíše jen nevhodným (nikoliv nesprávným) použitím koláčového grafu. Všimněme si v grafu 4, co se stane, když jsou si jednotlivé výseky (podíly) opticky příliš podobné. Jen těžko mezi nimi vidíme rozdíl. V takovém případě použití koláčového grafu postrádá smysl. Je úplně zbytečný, jeho prostřednictvím jsme se nic podstatného nedozvěděli. Lepší by patrně bylo zvolit sloupcový graf.
Druhým příkladem je vyloženě chybné použití koláčového grafu. Ty se používají k zobrazení podílů, ale pouze takových, které jsou součástí jednoho a téhož celku. Podívejme se na graf 5. Podkladem pro něj je podíl středoškolsky vzdělaných mužů (64 % ze všech 15letých a starších mužů) a podíl středoškolsky vzdělaných žen (57 % ze všech 15letých a starších žen). Nemáme tu jeden celek, který by mohl být zobrazen jako jeden koláč. Jsou tu dva koláče. Je zde 100 % mužů, z nichž 64 % má středoškolské vzdělání, a 100 % žen, z nichž 57 % má středoškolské vzdělání. Těch 64 % mužů a 57 % žen netvoří jeden koláč, nelze je do jednoho slepit. Pro tyto podíly je vhodný sloupcový graf, nikoliv koláčový. Už na první pohled jsme si chyby mohli všimnout: 64 % plus 57 % je přece 121 % (a to je víc než na jeden koláč).
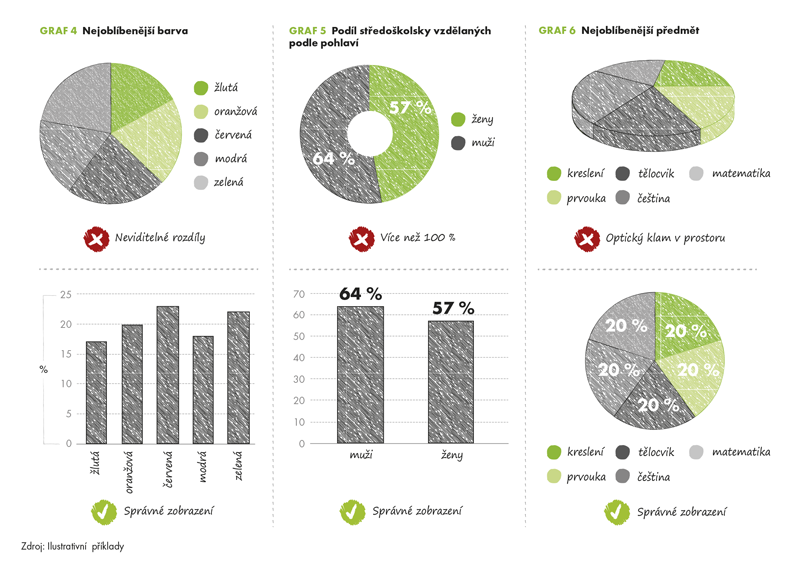
Posledním příkladem je ukázka optického klamu, který vzniká, pokud se u koláčových grafů použije perspektiva. Trojrozměrné grafy sice mohou působit zajímavěji, ale zobrazované údaje se jimi zkreslují. Když se podíváme na graf 6, zdá se, že nejoblíbenějším předmětem je tělocvik a nejméně oblíbená je matematika. Výsek, který představuje tělocvik, je opticky výrazně větší než výsek zachycující matematiku. A přitom tomu tak není. Každý výsek, který je v tomto grafu zobrazen, představuje 20% podíl (20 % dětí uvedlo jako nejoblíbenější matematiku, stejně jako jiných 20 % uvedlo tělocvik, češtinu, kreslení nebo prvouku). Pokud bychom v grafu zrušili prostorový pohled, bylo by to na první pohled jasné. Uživatel by si na prostorové grafy měl vždy dávat pozor, protože představují potenciální prostor pro záměrnou i nezáměrnou manipulaci s daty.
