Řetězení a zřetězené (srovnatelné) ceny
Občasný uživatel se s těmito pojmy a metodami obvykle přímo nesetká, a snad je ani nepotřebuje znát (i když používá jejich výsledky). Mohou však rozšířit jeho analytické možnosti. Nejde totiž o nic náročného, stačí na to selský rozum a násobilka.
Reálný růst ukazatele mezi dvěma roky (tzv. meziroční objemový index) již umíme vypočítat (ze stran 40–41 – vzpomeňme si na rozdíl mezi rostoucími výdaji za hrušky a skutečně snědenými hruškami). Díky meziročnímu objemovému indexu tedy víme, jak se spotřeba hrušek reálně vyvíjela z roku na rok, pak na další rok a další… Co když ale chceme vědět, jak se změnila za více let najednou, například mezi lety 2010 a 2012? Pokud známe jednotlivé po sobě jdoucí meziroční růsty (tj. z roku 2010 na 2011 a z roku 2011 na 2012 – viz tabulku C na stranách 90–91, řádek hrušky), pak není nic jednoduššího! Představme si to jako řetěz. Prvním článkem je rok 2010 a na něj navazují další články (roky). Když například víme, že mezi prvním článkem (rokem 2010) a druhým článkem řetězu (rokem 2011) vzrostla reálně spotřeba hrušek dvakrát, a následně mezi druhým a třetím článkem (z roku 2011 na 2012) opět dvakrát, pak můžeme vypočítat růst od začátku řetězu do jeho konce (tj. od roku 2010 do roku 2012). Stačí násobit reálné růsty mezi jednotlivými články (roky): 2,0 krát 2,0 = 4,0 (spotřeba mezi roky 2010 a 2012 vzrostla čtyřikrát). A pokud přidáme ještě jeden článek, rok 2013 (kdy jsme snědli 1,25krát víc hrušek než v roce 2012), pak je růst mezi roky 2010 a 2013: 2,0 krát 2,0 krát 1,25 = 5,0 (spotřeba reálně vzrostla pětkrát). A to je řetězení. Vcelku intuitivní záležitost.
Čísla utržená ze řetězu?
Ale pamatujme si, bylo by chybou, pokud bychom meziroční růsty sčítali! Je třeba je mezi sebou násobit, protože každý článek řetězu (rok) je základnou růstu následujícího článku (roku). A ještě jedna malá odbočka: metoda řetězení je obecná metoda práce s indexy. To znamená, že řetězit můžeme třeba i meziměsíční indexy inflace, abychom získali meziroční míru inflace. Nebo jakékoliv jiné (po sobě jdoucí a na sebe navazující) indexy vývoje.
A od řetězení je už jen krůček k dalšímu pojmu, který bychom měli znát – zřetězené ceny referenčního roku (například roku 2010). Někdy se nesprávně zaměňují za termín „stálé ceny“ (roku 2010) – základní rozdíly mezi těmito dvěma pojmy si vysvětlíme v poslední kapitole. Makroekonomické agregáty ve zřetězených (někdy také srovnatelných) cenách jsou obvykle publikovány jen jako doplněk k mnohem důležitějšímu ukazateli – k reálnému růstu. Jedná se o pomocné (doplňkové) údaje, které jsou zkonstruovány až následně, na závěr, s pomocí již vypočteného reálného růstu (nikoliv naopak). Samy o sobě nepřinášejí nic nového. Posuďte sami, k čemu je dobré vědět, kolik by byla (hypoteticky) spotřeba hrušek v roce 2013, kdyby se ceny nezměnily od roku 2010? Velkou informační hodnotu to nemá, že? Proč se tedy počítají a publikují?
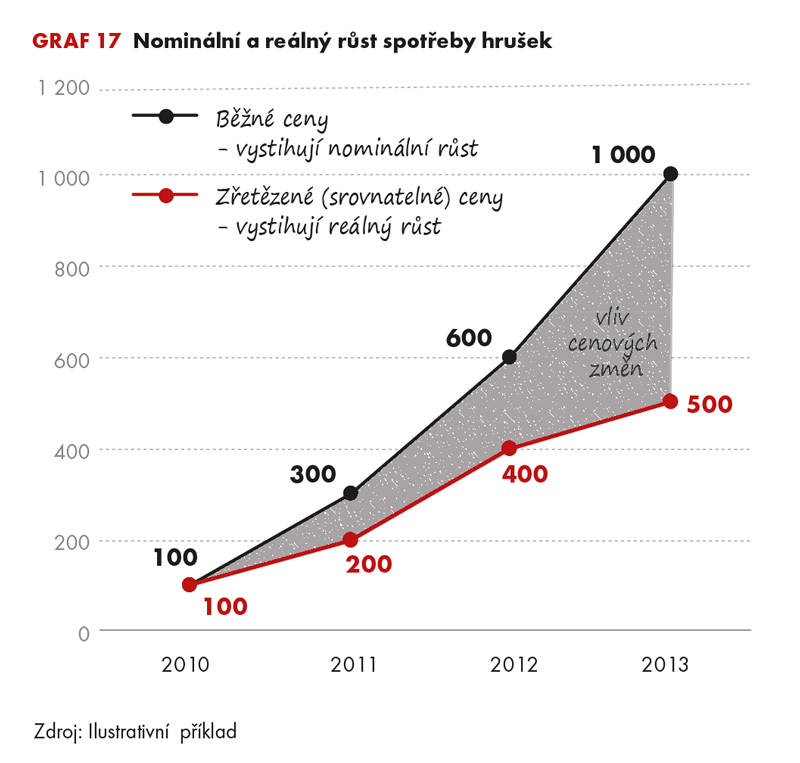
Síla tohoto ukazatele tkví v analytické rovině. Může nám zjednodušit analytickou práci. Díky němu můžeme například společně graficky vyjádřit reálný a nominální vývoj ukazatele (jak uvidíte v grafu 17) nebo rychle spočítat reálný růst/pokles mezi libovolnými obdobími, například mezi lety 2010 a 2013. Výše jsme toto spočítali zřetězením několika meziročních růstů, což je však u delších časových řad zbytečně zdlouhavé. S využitím údajů ve zřetězených cenách (roku 2010) stačí vydělit dva roky (třeba i hodně vzdálené), a výsledek máme hned.
Abychom pochopili, k čemu časové řady ve zřetězených cenách jsou, ukažme si na příkladu naší spotřeby hrušek, jak tyto údaje vznikají (pomohou nám tabulky na staně 90). K výpočtu celé řady nám stačí znát spotřebu hrušek v roce 2010 (100 Kč – tabulka A) a meziroční reálný růst v následujících letech – tabulka C.
Zalistujme zpět na strany 40–41. Vzpomínáte? Nominální růst lze rozdělit na reálný růst krát růst cen. A teď otázka: co získáme, pokud budeme spotřebu hrušek v roce 2010 (tj. 100 Kč) násobit výhradně reálnými růsty v následujících letech (tj. objemovými indexy) a růstu cen si vůbec nebudeme všímat? Přece spotřebu v jednotlivých letech v cenách roku 2010 (ceny se prostě od roku 2010 nezmění, když budeme brát v úvahu pouze objemové indexy)! Dejme se do počítání (výsledky najdeme přehledně na straně 90 v tabulce E, řádek hrušky). Spotřeba hrušek v roce 2011 v cenách roku 2010 bude mít hodnotu 200 Kč (100 krát 2,0). V roce 2012 se spotřeba opět meziročně reálně zdvojnásobila (ale už to není z těch původních 100, ale z 200 Kč v roce 2011), takže spotřeba v roce 2012 v cenách roku 2010 má hodnotu 400 (200 Kč krát 2,0). A analogicky dostaneme i výsledek pro rok 2013 (400 krát 1,25 = 500 Kč). Snadné, že? Výsledná časová řada spotřeby ve zřetězených cenách roku 2010 (100, 200, 400, 500) v sobě zachycuje pouze reálný růst „objemu“, nikoliv cen.
A teď tuto časovou řadu ve zřetězených (srovnatelných) cenách roku 2010 (tabulka E) můžeme využít k rychlejší práci. Snadno můžeme vypočítat reálný růst spotřeby hrušek například mezi lety 2010 a 2013. Stačí jednoduše porovnat tyto dva roky mezi sebou: 500 děleno 100 = 5,0. Rychlé, že? Pokud se publikují časové řady ve zřetězených cenách referenčního roku (jedno jakého), může uživatel snadno vypočítat to, co by pomocí řetězení dělal zbytečně dlouho. A zajímavé je i grafické využití těchto časových řad.
