Neaditivnost zřetězených cen
Pokud jsme o tématu předchozí kapitoly tvrdili, že je (z)běžný uživatel statistických dat příliš často nepotká, v tomto případě to platí ještě více. Ale jestliže jste dočetli až sem, zůstaňte. Zaměříme se sice na jedno z úskalí práce se zřetězenými cenami – na neaditivnost časových řad, ale také si na číselném příkladu zopakujeme vše, co jsme si doposud řekli o reálném růstu. A to s hromadou vzájemně propojených tabulek. Stačí otočit list na strany 90–91. Navážeme totiž na náš příklad ze stran 86–87 a z tabulek na straně 90. Teď už však neutrácíme jen za hrušky, ale i za pastelky. Celková spotřeba naší domácnosti je tak dána jejich součtem. Je to nová výzva. Naše spotřeba již není homogenní a zhodnocení růstu celkové spotřeby je složitější (než za samotné hrušky).
Když celek není součtem částí…
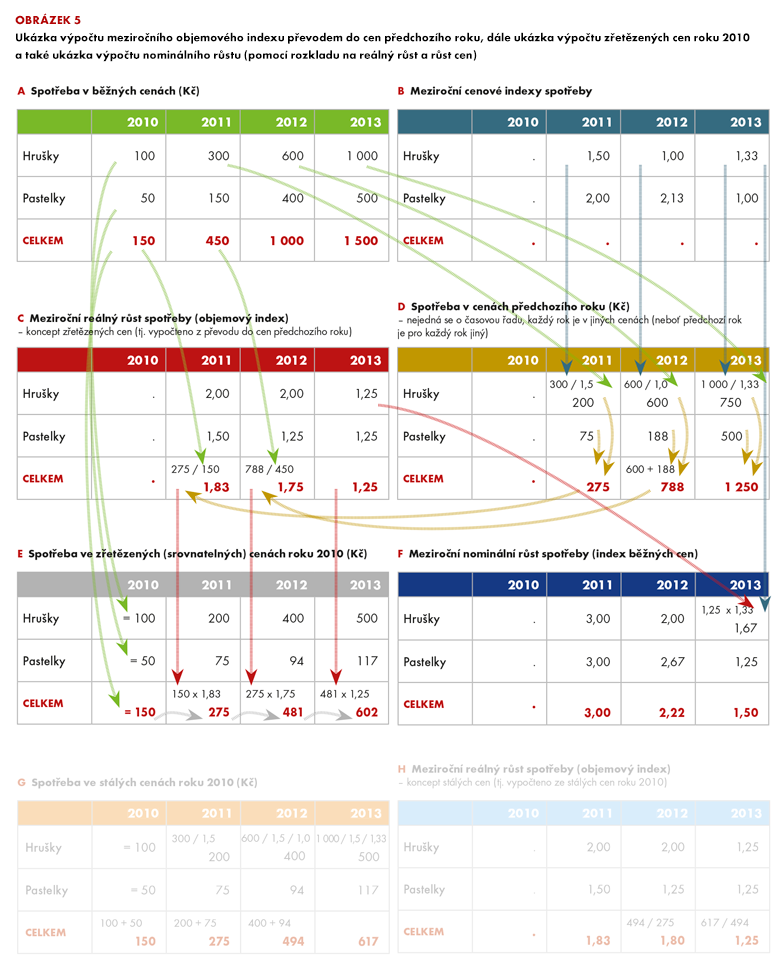
I v případě celkové spotřeby platí, že nominální růst (tj. růst v běžných cenách – tabulka F) nám neodpoví na otázku, zda jsme skutečně spotřebovali více, nebo méně (hrušek a pastelek). K tomu potřebujeme reálný růst (objemový index). Za hrušky jsme jej pro jeden rok vypočetli na stranách 40–41 – je třeba odstranit cenové změny mezi jednotlivými roky. Pamatujete? Totéž teď musíme (v celé časové řadě) udělat i za pastelky. Připomeňme si celý postup na roku 2011. Nejprve převedeme pastelky do cen předchozího roku (tj. do cen roku 2010). V roce 2011 jsme za ně utratili, jak vidíme v tabulce A, 150 Kč (tj. jedná se o pastelky v cenách roku 2011). Abychom je převedli do cen roku 2010, musíme odstranit růst cen mezi lety 2010 a 2011 (ten vidíme v tabulce B – ceny vzrostly 2krát). Spotřebu pastelek v roce 2011 v cenách roku 2010 pak vypočteme jako 150 děleno 2,0 = 75 Kč (v tabulce D). A objemový index za pastelky v roce 2011 (tj. reálný růst) už vypočteme rychle (tabulka C). Porovnáme naši spotřebu pastelek v roce 2011 (v cenách roku 2010) se spotřebou v roce 2010. Můžeme to udělat, protože obojí je ve stejných cenách, takže do indexu již nepromlouvá žádná změna cen. Čili 75 děleno 50 = 1,5 (v roce 2011 jsme tedy reálně spotřebovali o 50 % pastelek více než v roce 2010). A takto budeme pokračovat s každým rokem, zvlášť za hrušky a zvlášť za pastelky. A jak vypočteme reálný růst celkové spotřeby? Pouze tak, že sečteme pastelky a hrušky v cenách předchozího roku a tento součet porovnáme s celkovou spotřebou v předchozím roce (např. pro rok 2012: 788 děleno 450 = 1,75). Pamatujme si: k odhadu celkové spotřeby vždy potřebujeme znát dílčí složky v cenách předchozího roku. Proč? Protože těžko najdeme cenový index, jenž by v sobě zahrnoval cenový vývoj hrušek i pastelek a který bychom mohli použít k přímému přecenění celkové spotřeby do cen předchozího roku.
Když teď máme nejen spotřebu pastelek a hrušek v roce 2010 (tabulka A), ale i meziroční reálné růsty v následujících letech (tabulka C), pak můžeme pomocí řetězení, o kterém jsme hovořili na stranách 86–87, vypočítat spotřebu ve zřetězených (srovnatelných) cenách roku 2010 v celé časové řadě (tabulka E). Pro hrušky už jsme to udělali v předchozí kapitole, teď si to můžeme zopakovat za celkovou spotřebu. Připomeňme jen, že podstatou řetězení je to, že násobíme původní hodnotu z roku 2010 jednotlivými objemovými indexy (reálným růstem) za další a další rok. Například za rok 2011 je celková spotřeba ve zřetězených cenách roku 2010 vypočtena jako 150 krát 1,83, rok 2012 je roven (150 krát 1,83) krát 1,75 a rok 2013 je roven (150 krát 1,83 krát 1,75) krát 1,25 – každý rok prostě přidáváme další článek řetězu.

A tím se konečně dostáváme k tématu této kapitoly. Pokud se totiž podíváme na tabulku E, uvidíme, že v referenčním roce (2010) a následném roce (2011) se hrušky plus pastelky rovnají celkové spotřebě (100 + 50 = 150 nebo 200 + 75 = 275). Nicméně v letech 2012 a 2013 už to neplatí. Součet pastelek a hrušek neodpovídá celkové hodnotě spotřeby ve zřetězených cenách roku 2010. Údaje nejsou aditivní! Například v roce 2013 je celková spotřeba 602 Kč, zatímco součet hrušek a pastelek činí 617 Kč (500 plus 117).
Zřetězením každé řady zvlášť (hrušek, pastelek i celku!) vzniká rozdíl, který obvykle není příliš významný a nemá velký vliv na vypovídací schopnost, ale uživatelé jej musejí vzít v úvahu. Důvodem jeho vzniku jsou každoroční změny ve struktuře spotřeby. Jeden rok představuje útrata za pastelky 33 % (rok 2011), jindy 40 % (rok 2012). Tato změna struktury se při řetězení postupně promítá do hodnoty celkové spotřeby ve zřetězených cenách roku 2010. Připomeňme ještě jednou, že časová řada celkové spotřeby ve zřetězených cenách vzniká zcela odděleně od zřetězení hrušek a pastelek – jde o zřetězení objemových indexů celkové spotřeby, které vychází z převodu hrušek a pastelek do cen předchozího roku (nikoliv do cen roku 2010). Trochu složitěji řečeno, při řetězení celkové spotřeby dochází k násobení objemových indexů s každoročně odlišným poměrem mezi hruškami a pastelkami (tj. struktura celkové spotřeby v meziročním indexu 2011/2010 je jiná než v indexu 2012/2011), a proto není spotřeba v roce 2012 v cenách roku 2010 aditivní.
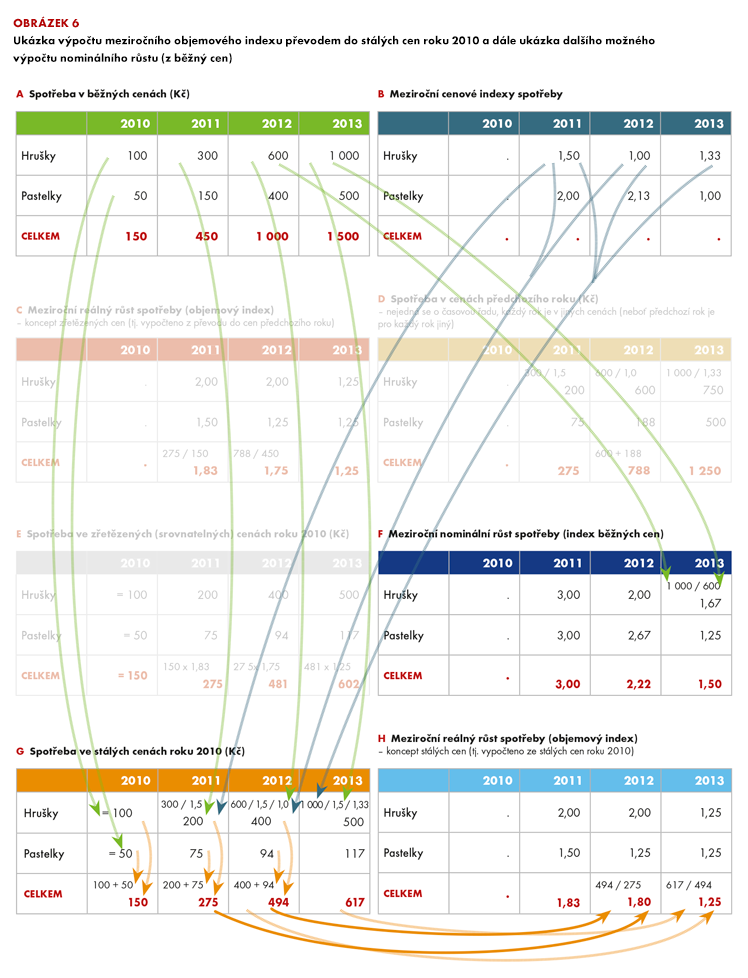
Z důvodu neaditivnosti tak nelze údaje ve zřetězených (srovnatelných) cenách využít pro zkoumání struktury, přestože jsou ideální pro analýzu vývoje ukazatelů v čase (hrušek, pastelek nebo celku). Pokud by se k analýze struktury použily, byla by to chyba. Toto omezení může mírně zkomplikovat práci uživatelů, například při výpočtu tzv. příspěvků k růstu, nemělo by je to však překvapit. Není to chyba, je to (jak jsme si tady řekli už mnohokrát) jen něco za něco. Velmi dobře vystihují reálný růst v podmínkách rychle se měnícího světa, a neaditivnost je cena, kterou za to musíme zaplatit.
